前言
"Paper 整理"系列只是試著將paper中的概念,或是將別人對paper的見解整理起來,幫助自己消化及日後複習。都會附上出處,如有侵權或錯誤煩請email告知:jason.eed05@gmail.com
論文連結
Semantic Segmentation (語義分割)
語義分割的任務是,給定一張圖片,經過語義分割後的結果就是一張包含若干種顏色的圖片。其中每一種顏色代表一個類別。
Semantic Segmentation in Street Scenes:
Paper 提到街景圖的語義分割,相比一般圖片的語義分割主要會多出兩個難題:
- 街景中物體有分遠近,故圖片中object 尺度會變化很大。一般 model 很難在圖片中某個範圍同時很好的分割大物體和小物體
- 街景的語義分割需要有很大的 "Receptive field"
Receptive field 是指一個feature 或output 會被多少個input pixel 影響,也就是可以"感知到"輸入圖片多大的範圍。
Receptive field 不夠大,就很容易偵測不到大物件。比如一輛車很靠近你,你卻看不出那是一輛車,因為你的感知範圍太小了,一次只能看到車子的某個部分。這有點像瞎子摸象的概念,因為感受的範圍有限(大象的某個部位)所以看不出整體(一頭大象)
Related Work
CNN->FCN
原始的CNN是由convolutional layer, pooling, and fully connect layer 所構成。因為FC層,CNN最後的結果常會是一維的(ex. 每個類別各給一個機率值做圖片分類)
FCN (Fully Convolutional Network) 則是捨棄 FC layer,只剩下convolutional layer, pooling 等的tensor 運算,其輸出就可以是多維的,並可以控制成每個類別一個二維map,代表圖片每個位置於某類別的機率。FCN 就是因此在之前被廣為運用在語義分割這類應用上。
( CNN(上) 與 FCN(下)的比較 )
Pooling layer 的問題
CNN, FCN 中的 pooling layer 原本是用以提取"重點資訊"並以此擷取更高 level 的feature。
feature 的 level 舉例: 以一張貓的圖片為例,曲線、形狀屬於較低level;貓的腳、一隻貓屬於較高 level。
但是因為pooling layer 的 "提取重點",原本input 關於位置的訊息也會減少,最後如果要 up-sampling 或 deconvolution 的話結果也會不夠精細,accuracy 上不去。
Atrous Convolution (空洞捲積)

( 一般convolution(左) 與atrous convolution(右) )
source: https://towardsdatascience.com/review-dilated-convolution-semantic-segmentation-9d5a5bd768f5
一種解決pooling layer 所帶來問題的方式,是用空洞捲積代替pooling。空洞捲積和一般捲積一樣,只是在做捲積時中間會有擴張 (dilation)。
以一維來看,可以用以下圖片和公式幫助理解。式中d為擴張程度dilation rate:
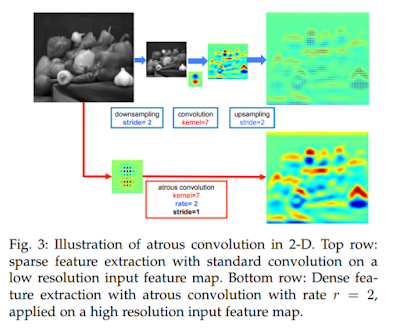
因為空洞捲積沒有down-sampling 的動作,所以自然不需要up-sampling,也可以少掉up-sampling 所帶來的失真(可參考下圖)。
from: https://arxiv.org/pdf/1606.00915.pdf
此外因為atrous convolution 中間有擴張,所以同樣有pooling 提取higher level feature 的特性。
另外他的另一個好處,是比一般捲積層的感受範圍還要大些。以上面的動畫為例,右邊的空洞捲積可以看為5X5大小的捲積,只是擴張的部分權重是零。
dilation rate 越大,感受野越廣。但是也不能一味的擴張(像下面),不然paper 說捲積效果會變ineffective。
(不過paper 中dilation rate 有用到二十幾三十,所以其實以比例尺來看下面的kernel 其實是可以接受的?)
擴張 Receptive Field
另一個提升RF 的方法是在model 中加入更多層的convolutional layer。
以下面的例子來看,一個5X5 input size 經過兩次3X3 kernel,no padding & stride=1 的捲積下,最後的output 會是1X1。我們可以觀察,經過一次convolution 的每個output 感受範圍是3X3 (圖中粉紅色和淺藍色的部分),但再經過一次convolution,最右邊的output 便可感受到整個5X5 的input 了。
Paper 中有給一個公式,假設兩捲積的RF 分別是K1, K2,串接 (cascade) 在一起的RF 便會是 K1+K2-1。讀者可以用下面的例子加以驗證。
但也不能單純加太多層,不然會有gradient vanishing 等問題。
於是這篇paper 引用了 DenseNet 這個related work。其主要的理念是讓每層 layer 的輸入都是其之前每層layer 的 output。如此極致發揮 residual 理念的架構,自然在 gradient vanishing 方面解決得不錯。
Multi-size Detection: ASPP
Atrous Spatial Pyramid Pooling (ASPP) ,即有空洞捲積的金字塔結構 Pooling。此為對同一個 input feature,使用不同 dilation rate 的空洞捲積去處理它,並將得到的各個結果 concate
在一起(parallel)。之後可能再透過 1X1 conv 控制 channel 數。
至於 related work 中提到 ASPP 的原因,是因為它在 multi-size detection 上有所表現。
Dense Atrous Spatial Pyramid Pooling (DenseASPP)
想法
Increase receptive field + multi-size detection ->
架構中既要有 DenseNet 的骨架 (cascade) 、 又要同時有 ASPP 的骨架!
架構
此架構融合了 cascade (藍色箭頭) 以及 parallel (紅色箭頭) 的特性,所以此 paper 表示它在 increase receptive field & multi-size detection 上都應該表現不錯。
減少參數:1X1 conv
我們可以看到,隨著後面 atrous convolution layer 的 input (前面層的 output concate) 越來越多,channel 也會越來越多。為了減少其中所需要的參數以及控制 input channel 數 (paper 中將它從原本 $C_l$ 減少到 $C_0/2$),我們在將 input 送進 atrous conv 前會先經過 1X1 conv
式中 L 為 DenseASPP 中 atrous layer 數,K為 kernel size。
如果沒有1X1 conv 的話參數數量可能就要有 $S=\sum_{l=1}^L [C_l \times K^2 \times n] $ 個。
設 $n=C_0/8$ for all layers in DenseASPP,則 DenseASPP 參數數量為:
如果沒有1X1 conv 的話參數數量可能就要有 $S=\sum_{l=1}^L [C_l \times K^2 \times n] $ 個。




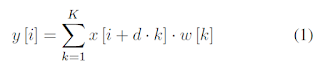










沒有留言:
張貼留言